「FTL珍珠砲」：修訂間差異

於 2024年9月5日 (四) 15:07 的最新修訂

FTL(Fast Than Light)中文珍珠砲，最初是由scicarft伺服器中玩家Xcom6000所開發，藉由數量可觀的TNT

同時對終界珍珠轟炸而累積大量動能，最後發射而出使玩家可以在不到一秒的時間旅行至千萬格外，成功打破MINECRAFT遊戲中限制的320格每秒的速度限制。

In Minecraft the theoretical speed limit is known to be 320m/s
One object has been known to break this law--projectiles

--Xcom6000

FTL結構[編輯 | 編輯原始碼]

一台完整的FTL大致可以分為以下幾個部件2D單選面板、TNT數量控制、終界珍珠滯留裝置、TNT複製陣列、區塊加載裝置。

2D單選面板[編輯 | 編輯原始碼]

此結構提供了玩家一個2D的地點選擇面板，按下選擇地點後面板將會把預先設定好的TNT數量、發射方位角

一併透過脈波的形式將訊號傳送至頂端的TNT陣列進行設定。

TNT數量控制[編輯 | 編輯原始碼]

假設單一最大的陣列可以一次複製588個TNT以供發射，為了精準控制發射所需的TNT數量，通常會將不同複製數量的TNT陣列以小排到大的形式組成FTL的一側陣列，且可以依照所需的TNT發射數量來進行設定588到1個TNT數量的控制。

終界珍珠滯留裝置[編輯 | 編輯原始碼]

玩家投擲終界珍珠後會透過半線勾觸發訊號，活塞將終界珍珠的隨機動量X、Y、Z給消除掉方便後續發射時不會產生任何的座標偏差。

TNT複製陣列[編輯 | 編輯原始碼]

是FTL中最核心的一部分，在FTL工作時陣列通常會複製兩個批次的TNT，第一個批次的TNT通常數量較少只為了將第二批次的TNT給加速到FTL正中央。

通常越多的TNT複製數量決定著後續發射精準度。

區塊加載裝置[編輯 | 編輯原始碼]

在FTL發射的同時區塊加載裝置會啟動，並瞬間加載每次終界珍珠停留的位置。

TNT爆炸解釋[編輯 | 編輯原始碼]

TNT爆炸[編輯 | 編輯原始碼]

在TNT點然後會馬上變成一個實體方塊，大小為0.98x0.98x0.98，同時對Y軸施加0.2block/tick的動能使TNT往上彈跳

與隨機分佈在X、Z軸上合力為0.2block/tick的動能，並且在80個gt後引爆，爆炸的中心點位於TNT中心點

往上0.0625格高度，如右圖所示黃色點為起爆點中心。

在每次TNT爆炸時會去以爆炸中心往外進行4096次所有可能的爆炸射線計算，並且最後只會有1352條爆炸射線被保留。

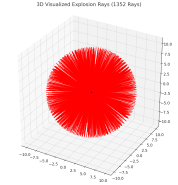
1352條射線計算方式：

一個面有16x16x16＝256個點

方塊6個面的總點數：6x256＝1536個點

多餘的角：8x2＝16個點

多餘的邊：12*14＝168個點

最後可得出

1536-16-168＝1352個爆炸射線

TNT爆炸作用實體的推力[編輯 | 編輯原始碼]

TNT爆炸產生的推力會從TNT中心底部往上0.0625格高度開始往外計算，且實體受到推力的大小

是取決於實體碰撞箱中心底部距離爆炸中心的距離來決定，而最後實體的推力會作用於眼部高度。

黃色是爆炸射線、藍色是實體眼部高度 (eye height)、紅色是最後推力的作用地點

最後使終界珍珠盡可能的靠近TNT爆炸中心點以獲得最大的推力，在最完美的矯正下（最近的距離）

每顆TNT可以對終界珍珠造成0.864block/tick的加速度。

也就是說如果你在地獄同時使用4340278顆TNT對終界珍珠轟炸所產生的推力可以在1/20秒內把你送到，3750000格外的地方
也就是等於在主世界直達邊界。

發射角度與TNT數量計算方式[編輯 | 編輯原始碼]

為了實現360度的發射通常會複製兩個批次的TNT並且排列成如右圖所示，控制兩組TNT的數量來實現360度發射。

以下情況極度簡化計算會根據每台FTL型態不同而有不一樣的計算方式

且忽略了終界珍珠的飛行阻力與地心引力。

兩組TNT數量大致的計算方式如下
已知條件：
初始終界珍珠位置：（x1,y1）
發射目標位置：（x2,y2）

兩側TNT起爆點中心位置：TNT1（a,b) TNT2(c,d)

首先可以定義出兩側TNT對於終界珍珠的推力向量V1、V2

$\mathbf {v} _{1}=\langle a-x_{1},b-y_{1}\rangle$

$\mathbf {v} _{2}=\langle c-x_{1},d-y_{1}\rangle$

接著是計算初始終界珍珠位置到目標位置所需多少推力向量V_target

$\mathbf {v} _{\text{target}}=\langle x_{2}-x_{1},y_{2}-y_{1}\rangle$

接著就可以將V1、V2向量合成得出結果，n1、n2則是兩側TNT數量其中，V_result必須與V_target相等

$\mathbf {v} _{\text{result}}=n_{1}\mathbf {v} _{1}+n_{2}\mathbf {v} _{2}$

然後將向量拆分成x與y兩個來計算，就可以得到以下方程式

$n_{1}\times (a-x_{1})+n_{2}\times (c-x_{1})=x_{2}-x_{1}$

$n_{1}\times (b-y_{1})+n_{2}\times (d-y_{1})=y_{2}-y_{1}$

最後求解寫成矩陣形式，就可以得到最後的解n1、n2 即為兩側TNT分別數量

${\begin{pmatrix}a-x_{1}&c-x_{1}\\b-y_{1}&d-y_{1}\end{pmatrix}}{\begin{pmatrix}n_{1}\\n_{2}\end{pmatrix}}={\begin{pmatrix}x_{2}-x_{1}\\y_{2}-y_{1}\end{pmatrix}}$

${\begin{pmatrix}n_{1}\\n_{2}\end{pmatrix}}={\begin{pmatrix}a-x_{1}&c-x_{1}\\b-y_{1}&d-y_{1}\end{pmatrix}}^{-1}{\begin{pmatrix}x_{2}-x_{1}\\y_{2}-y_{1}\end{pmatrix}}$

@@ 行 66： / 行 66： @@
 [[檔案:TNT與終界珍珠 推力關係.png|左|縮圖|TNT與終界珍珠推力關係|邊框]]
  黃色是爆炸射線、藍色是實體眼部高度 (eye height)、紅色是最後推力的作用地點
@@ 行 88： / 行 91： @@
 == 發射角度與TNT數量計算方式 ==
- 為了實現360度的發射通常會複製兩個批次的TNT並且排列成如 下 圖所示，控制兩組TNT的數量來實現360度發射。
+ 為了實現360度的發射通常會複製兩個批次的TNT並且排列成如 右 圖所示，控制兩組TNT的數量來實現360度發射。[[檔案:發射角度.png|縮圖|190x190px|珍珠發射角度]]
-[[檔案:發射角度.png|縮圖|200x200像素|珍珠發射角度|左]]
@@ 行 104： / 行 105： @@
 '''以下情況極度簡化計算會根據每台FTL型態不同而有不一樣的計算方式'''
-'''且忽略了終界珍珠的飛行阻力與地心引力。'''
+'''且忽略了終界珍珠的飛行阻力與地心引力。'''<blockquote>''兩組TNT數量大致的計算方式如下''
-<blockquote>''兩組TNT數量大致的計算方式如下''
 ''已知條件：''
@@ 行 116： / 行 115： @@
 ''兩側TNT起爆點中心位置：TNT1（a,b) TNT2(c,d)''</blockquote>
   首先可以定義出兩側TNT對於終界珍珠的推力向量V1、V2
-[[檔案:Tnt1tnt2向量計算.png|左|無框|169x169像素]]
+<math>\mathbf{v}_1 = \langle a - x_1, b - y_1 \rangle
+</math>
+<math>\mathbf{v}_2 = \langle c - x_1, d - y_1 \rangle
+</math>
   接著是計算初始終界珍珠位置到目標位置所需多少推力向量V_target
-[[檔案:目標 向量.png|左|無框|298x298像素]]
+<math>\mathbf{v}_{\text{target}} = \langle x_2 - x_1, y_2 - y_1 \rangle
+</math><blockquote>接著就可以將V1、V2 向量 合成得出結果，n1、n2則是兩側TNT數量其中，V_result必須與V_target相等</blockquote><math>\mathbf{v}_{\text{result}} = n_1 \mathbf{v}_1 + n_2 \mathbf{v}_2
-<blockquote>接著就可以將V1、V2向量合成得出結果，n1、n2則是兩側TNT數量其中，V_result必須與V_target相等</blockquote>[[檔案:合成向量結果.png|無框]]
+</math>
   然後將向量拆分成x與y兩個來計算，就可以得到以下方程式
-[[檔案:兩側tnt分解方程.png|左|無框|296x296像素]]
+<math>n_1 \times (a - x_1) + n_2 \times (c - x_1) = x_2 - x_1
+</math>
+<math>
+n_1 \times (b - y_1) + n_2 \times (d - y_1) = y_2 - y_1
+</math>
   最後求解寫成矩陣形式，就可以得到最後的解n1、n2 即為兩側TNT分別數量
-[[檔案:轉換矩陣形式.png|左|無框]]
+<math>\begin{pmatrix}
-[[檔案:線性方程組解.png|左|無框]]
+a - x_1 & c - x_1 \\
+b - y_1 & d - y_1
+\end{pmatrix}
+\begin{pmatrix}
+n_1 \\
+n_2
+\end{pmatrix}
+=
+\begin{pmatrix}
+x_2 - x_1 \\
+y_2 - y_1
+\end{pmatrix}
+</math>
+<math>\begin{pmatrix}
+n_1 \\
+n_2
+\end{pmatrix}
+=
+\begin{pmatrix}
+a - x_1 & c - x_1 \\
+b - y_1 & d - y_1
+\end{pmatrix}^{-1}
+\begin{pmatrix}
+x_2 - x_1 \\
+y_2 - y_1
+\end{pmatrix}
+</math>